We show that all self-adjoint extensions of semibounded Sturm–Liouville operators with limit-circle endpoint(s) can be obtained via an additive singular form-bounded self-adjoint perturbation of rank equal to the deficiency indices, say 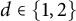. This characterization generalizes the well-known analog for semibounded Sturm–Liouville operators with regular endpoints. Explicitly, every self-adjoint extension of the minimal operator can be written as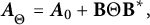

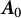where is a distinguished self-adjoint extension and is a self-adjoint linear relation in 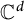. The perturbation is singular in the sense that it does not belong to the underlying Hilbert space but is form-bounded with respect to 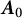, i.e., it belongs to 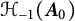, with possible “infinite coupling.” A boundary triple and compatible boundary pair for the symmetric operator are constructed to ensure that the perturbation is well defined and self-adjoint extensions are in a one-to-one correspondence with self-adjoint relations .

The merging of boundary triples with perturbation theory provides a more holistic view of the operator’s matrix-valued spectral measures: identifying not just the location of the spectrum, but also certain directional information.

As an example, self-adjoint extensions of the classical Jacobi differential equation (which has two limit-circle endpoints) are obtained, and their spectra are analyzed with tools both from the theory of boundary triples and perturbation theory.