We use Stein’s method to establish the rates of normal approximation in terms of the total variation distance for a large class of sums of score functions of samples arising from random events driven by a marked Poisson point process on 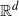 . As in the study under the weaker Kolmogorov distance, the score functions are assumed to satisfy stabilisation and moment conditions. At the cost of an additional non-singularity condition, we show that the rates are in line with those under the Kolmogorov distance. We demonstrate the use of the theorems in four applications: Voronoi tessellations, k-nearest-neighbours graphs, timber volume, and maximal layers.
. As in the study under the weaker Kolmogorov distance, the score functions are assumed to satisfy stabilisation and moment conditions. At the cost of an additional non-singularity condition, we show that the rates are in line with those under the Kolmogorov distance. We demonstrate the use of the theorems in four applications: Voronoi tessellations, k-nearest-neighbours graphs, timber volume, and maximal layers.
Mathematics
