Let 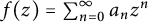be an entire function on the complex plane, and let 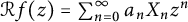be its randomization induced by a standard sequence 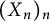of independent Bernoulli, Steinhaus, or Gaussian random variables. In this paper, we characterize those functions 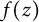such that 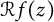is almost surely in the Fock space 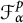for any 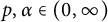. Then such a characterization, together with embedding theorems which are of independent interests, is used to obtain a Littlewood-type theorem, also known as regularity improvement under randomization within the scale of Fock spaces. Other results obtained in this paper include: (a) a characterization of random analytic functions in the mixed-norm space 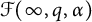, an endpoint version of Fock spaces, via entropy integrals; (b) a complete description of random lacunary elements in Fock spaces; and (c) a complete description of random multipliers between different Fock spaces.