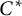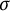The classical Gelfand–Naimark theorems provide important insight into the structure of general and of commutative -algebras. It is shown that these can be generalized to certain ordered -algebras. More precisely, for -bounded closed ordered -algebras, a faithful representation as operators is constructed. Similarly, for commutative such algebras, a faithful representation as complex-valued functions is constructed if an additional necessary regularity condition is fulfilled. These results generalize the Gelfand–Naimark representation theorems to classes of -algebras larger than 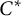-algebras, and which especially contain -algebras of unbounded operators. The key to these representation theorems is a new result for Archimedean ordered vector spaces V: If V is 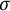-bounded, then the order of V is induced by the extremal positive linear functionals on V.