We compute the generator rank of a subhomogeneous 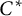 -algebra in terms of the covering dimension of the pieces of its primitive ideal space corresponding to irreducible representations of a fixed dimension. We deduce that every
-algebra in terms of the covering dimension of the pieces of its primitive ideal space corresponding to irreducible representations of a fixed dimension. We deduce that every 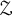 -stable approximately subhomogeneous algebra has generator rank one, which means that a generic element in such an algebra is a generator.
-stable approximately subhomogeneous algebra has generator rank one, which means that a generic element in such an algebra is a generator.
This leads to a strong solution of the generator problem for classifiable, simple, nuclear 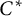 -algebras: a generic element in each such algebra is a generator. Examples of Villadsen show that this is not the case for all separable, simple, nuclear
-algebras: a generic element in each such algebra is a generator. Examples of Villadsen show that this is not the case for all separable, simple, nuclear 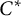 -algebras.
-algebras.
