We analyze the long-term stability of a stochastic model designed to illustrate the adaptation of a population to variation in its environment. A piecewise deterministic process modeling adaptation is coupled to a Feller logistic diffusion modeling population size. As the individual features in the population become further away from the optimal ones, the growth rate declines, making population extinction more likely. Assuming that the environment changes deterministically and steadily in a constant direction, we obtain the existence and uniqueness of the quasi-stationary distribution, the associated survival capacity, and the Q-process. Our approach also provides several exponential convergence results (in total variation for the measures). From this synthetic information, we can characterize the efficiency of internal adaptation (i.e. population turnover from mutant invasions). When the latter is lacking, there is still stability, but because of the high level of population extinction. Therefore, any characterization of internal adaptation should be based on specific features of this quasi-ergodic regime rather than the mere existence of the regime itself.

Copulas provide a powerful and flexible tool for modeling the dependence structure of random vectors, and they have many applications in finance, insurance, engineering, hydrology, and other fields. One well-known class of copulas in two dimensions is the Farlie–Gumbel–Morgenstern (FGM) copula, since its simple analytic shape enables closed-form solutions to many problems in applied probability. However, the classical definition of the high-dimensional FGM copula does not enable a straightforward understanding of the effect of the copula parameters on the dependence, nor a geometric understanding of their admissible range. We circumvent this issue by analyzing the FGM copula from a probabilistic approach based on multivariate Bernoulli distributions. This paper examines high-dimensional exchangeable FGM copulas, a subclass of FGM copulas. We show that the dependence parameters of exchangeable FGM copulas can be expressed as a convex hull of a finite number of extreme points. We also leverage the probabilistic interpretation to develop efficient sampling and estimating procedures and provide a simulation study. Throughout, we discover geometric interpretations of the copula parameters that assist one in decoding the dependence of high-dimensional exchangeable FGM copulas.

We consider a simple random walk on 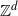started at the origin and stopped on its first exit time from 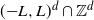. Write L in the form 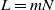with 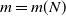and N an integer going to infinity in such a way that 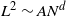for some real constant 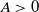. Our main result is that for 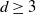, the projection of the stopped trajectory to the N-torus locally converges, away from the origin, to an interlacement process at level 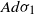, where 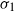is the exit time of a Brownian motion from the unit cube 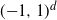that is independent of the interlacement process. The above problem is a variation on results of Windisch (2008) and Sznitman (2009).

We consider Poisson hail models and characterize up to boundaries the collection of critical moments which guarantee stability. In particular, we treat the case of infinite speed of propagation.

Consider the following migration process based on a closed network of N queues with 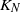customers. Each station is a /M/ queue with service (or migration) rate 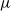. Upon departure, a customer is routed independently and uniformly at random to another station. In addition to migration, these customers are subject to a susceptible–infected–susceptible (SIS) dynamics. That is, customers are in one of two states: I for infected, or S for susceptible. Customers can swap their state either from I to S or from S to I only in stations. More precisely, at any station, each susceptible customer becomes infected with the instantaneous rate 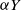if there are Y infected customers in the station, whereas each infected customer recovers and becomes susceptible with rate 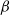. We let N tend to infinity and assume that 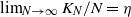, where 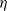is a positive constant representing the customer density. The main problem of interest concerns the set of parameters of such a system for which there exists a stationary regime where the epidemic survives in the limiting system. The latter limit will be referred to as the thermodynamic limit. We use coupling and stochastic monotonicity arguments to establish key properties of the associated Markov processes, which in turn allow us to give the structure of the phase transition diagram of this thermodynamic limit with respect to 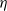. The analysis of the Kolmogorov equations of this SIS model reduces to that of a wave-type PDE for which we have found no explicit solution. This plain SIS model is one among several companion stochastic processes that exhibit both random migration and contagion. Two of them are discussed in the present paper as they provide variants to the plain SIS model as well as some bounds and approximations. These two variants are the departure-on-change-of-state (DOCS) model and the averaged-infection-rate (AIR) model, which both admit closed-form solutions. The AIR system is a classical mean-field model where the infection mechanism based on the actual population of infected customers is replaced by a mechanism based on some empirical average of the number of infected customers in all stations. The latter admits a product-form solution. DOCS features accelerated migration in that each change of SIS state implies an immediate departure. This model leads to another wave-type PDE that admits a closed-form solution. In this text, the main focus is on the closed stochastic networks and their limits. The open systems consisting of a single station with Poisson input are instrumental in the analysis of the thermodynamic limits and are also of independent interest. This class of SIS dynamics has incarnations in virtually all queueing networks of the literature.

A bootstrap percolation process on a graph with n vertices is an ‘infection’ process evolving in rounds. Let 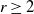be fixed. Initially, there is a subset of infected vertices. In each subsequent round, every uninfected vertex that has at least r infected neighbors becomes infected as well and remains so forever.

We consider this process in the case where the underlying graph is an inhomogeneous random graph whose kernel is of rank one. Assuming that initially every vertex is infected independently with probability 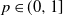, we provide a law of large numbers for the size of the set of vertices that are infected by the end of the process. Moreover, we investigate the case 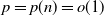, and we focus on the important case of inhomogeneous random graphs exhibiting a power-law degree distribution with exponent 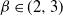. The first two authors have shown in this setting the existence of a critical 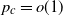such that, with high probability, if 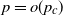, then the process does not evolve at all, whereas if 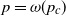, then the final set of infected vertices has size 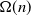. In this work we determine the asymptotic fraction of vertices that will eventually be infected and show that it also satisfies a law of large numbers.

We propose a modification to the random destruction of graphs: given a finite network with a distinguished set of sources and targets, remove (cut) vertices at random, discarding components that do not contain a source node. We investigate the number of cuts required until all targets are removed, and the size of the remaining graph. This model interpolates between the random cutting model going back to Meir and Moon (J. Austral. Math. Soc. 11, 1970) and site percolation. We prove several general results, including that the size of the remaining graph is a tight family of random variables for compatible sequences of expander-type graphs, and determine limiting distributions for binary caterpillar trees and complete binary trees.