During an epidemic outbreak, typically only partial information about the outbreak is known. A common scenario is that the infection times of individuals are unknown, but individuals, on displaying symptoms, are identified as infectious and removed from the population. We study the distribution of the number of infectives given only the times of removals in a Markovian susceptible–infectious–removed (SIR) epidemic. Primary interest is in the initial stages of the epidemic process, where a branching (birth–death) process approximation is applicable. We show that the number of individuals alive in a time-inhomogeneous birth–death process at time 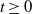, given only death times up to and including time t, is a mixture of negative binomial distributions, with the number of mixing components depending on the total number of deaths, and the mixing weights depending upon the inter-arrival times of the deaths. We further consider the extension to the case where some deaths are unobserved. We also discuss the application of the results to control measures and statistical inference.

Consider a two-type Moran population of size N with selection and mutation, where the selective advantage of the fit individuals is amplified at extreme environmental conditions. Assume selection and mutation are weak with respect to N, and extreme environmental conditions rarely occur. We show that, as 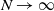, the type frequency process with time sped up by N converges to the solution to a Wright–Fisher-type SDE with a jump term modeling the effect of the environment. We use an extension of the ancestral selection graph (ASG) to describe the genealogical picture of the model. Next, we show that the type frequency process and the line-counting process of a pruned version of the ASG satisfy a moment duality. This relation yields a characterization of the asymptotic type distribution. We characterize the ancestral type distribution using an alternative pruning of the ASG. Most of our results are stated in annealed and quenched form.

We study a stochastic differential equation with an unbounded drift and general Hölder continuous noise of order 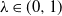. The corresponding equation turns out to have a unique solution that, depending on a particular shape of the drift, either stays above some continuous function or has continuous upper and lower bounds. Under some mild assumptions on the noise, we prove that the solution has moments of all orders. In addition, we provide its connection to the solution of some Skorokhod reflection problem. As an illustration of our results and motivation for applications, we also suggest two stochastic volatility models which we regard as generalizations of the CIR and CEV processes. We complete the study by providing a numerical scheme for the solution.

Suppose that m drivers each choose a preferred parking space in a linear car park with n spots. In order, each driver goes to their chosen spot and parks there if possible, and otherwise takes the next available spot if it exists. If all drivers park successfully, the sequence of choices is called a parking function. Classical parking functions correspond to the case .

We investigate various probabilistic properties of a uniform parking function. Through a combinatorial construction termed a parking function multi-shuffle, we give a formula for the law of multiple coordinates in the generic situation 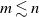. We further deduce all possible covariances: between two coordinates, between a coordinate and an unattempted spot, and between two unattempted spots. This asymptotic scenario in the generic situation 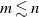is in sharp contrast with that of the special situation .

A generalization of parking functions called interval parking functions is also studied, in which each driver is willing to park only in a fixed interval of spots. We construct a family of bijections between interval parking functions with n cars and n spots and edge-labeled spanning trees with 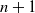vertices and a specified root.