We define a class of invariants, which we call homological invariants, for persistence modules over a finite poset. Informally, a homological invariant is one that respects some homological data and takes values in the free abelian group generated by a finite set of indecomposable modules. We focus in particular on groups generated by “spread modules,” which are sometimes called “interval modules” in the persistence theory literature. We show that both the dimension vector and rank invariant are equivalent to homological invariants taking values in groups generated by spread modules. We also show that the free abelian group generated by the “single-source” spread modules gives rise to a new invariant which is finer than the rank invariant.

For every minimal one-sided shift space X over a finite alphabet, left special elements are those points in X having at least two preimages under the shift operation. In this paper, we show that the Cuntz–Pimsner -algebra has nuclear dimension when X is minimal and the number of left special elements in X is finite. This is done by describing concretely the cover of X, which also recovers an exact sequence, discovered before by Carlsen and Eilers.

It is shown that the colored isomorphism class of a unital, simple, -stable, separable amenable C-algebra satisfying the universal coefficient theorem is determined by its tracial simplex.

We introduce interpolated multiple Hurwitz polylogs and interpolated multiple Hurwitz zeta values. In addition, we discuss the generating functions for the sum of the polylogs/zeta values of fixed weight, depth, and all heights. The functions are expressed in terms of generalized hypergeometric functions. Compared with the pioneering results of Ohno and Zagier on the generating function, our setup generalizes the results in three directions, namely, at general heights, with a t-interpolation, and as a Hurwitz type. As an application, by fixing the Hurwitz parameter to rational numbers, the generating functions for multiple zeta values with level are given.

We prove Fermat’s Last Theorem over and for prime exponents in certain congruence classes modulo by using a combination of the modular method and Brauer–Manin obstructions explicitly given by quadratic reciprocity constraints. The reciprocity constraint used to treat the case of is a generalization to a real quadratic base field of the one used by Chen and Siksek. For the case of , this is insufficient, and we generalize a reciprocity constraint of Bennett, Chen, Dahmen, and Yazdani using Hilbert symbols from the rational field to certain real quadratic fields.

Motivated by the desire to understand the geometry of the basic loci in the reduction of Shimura varieties, we study their “group-theoretic models”—generalized affine Deligne–Lusztig varieties—in cases where they have a particularly nice description. Continuing the work of Görtz and He (2015, Cambridge Journal of Mathematics 3, 323–353) and Görtz, He, and Nie (2019, Peking Mathematical Journal 2, 99–154), we single out the class of cases of Coxeter type, give a characterization in terms of the dimension, and obtain a complete classification. We also discuss known, new, and open cases from the point of view of Shimura varieties/Rapoport–Zink spaces.

In Kiukas, Lahti, and Ylinen (2006, Journal of Mathematical Physics 47, 072104), the authors asked the following general question. When is a positive operator measure projection valued? A version of this question formulated in terms of operator moments was posed in Pietrzycki and Stochel (2021, Journal of Functional Analysis 280, 109001). Let T be a self-adjoint operator, and let F be a Borel semispectral measure on the real line with compact support. For which positive integers 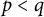do the equalities 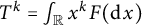, , 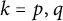imply that F is a spectral measure? In the present paper, we completely solve the second problem. The answer is affirmative if 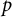is odd and 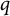is even, and negative otherwise. The case 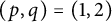closely related to intrinsic noise operator was solved by several authors including Kruszyński and de Muynck, as well as Kiukas, Lahti, and Ylinen. The counterpart of the second problem concerning the multiplicativity of unital positive linear maps on 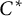-algebras is also provided.

Adjacent dyadic systems are pivotal in analysis and related fields to study continuous objects via collections of dyadic ones. In our prior work (joint with Jiang, Olson, and Wei), we describe precise necessary and sufficient conditions for two dyadic systems on the real line to be adjacent. Here, we extend this work to all dimensions, which turns out to have many surprising difficulties due to the fact tha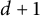t , not 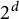, grids is the optimal number in an adjacent dyadic system in 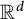. As a byproduct, we show that a collection of 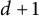dyadic systems in 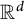is adjacent if and only if the projection of any two of them onto any coordinate axis are adjacent on 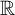. The underlying geometric structures that arise in this higher-dimensional generalization are interesting objects themselves, ripe for future study; these lead us to a compact, geometric description of our main result. We describe these structures, along with what adjacent dyadic (and n-adic, for any n) systems look like, from a variety of contexts, relating them to previous work, as well as illustrating a specific exa.

Let 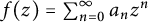be an entire function on the complex plane, and let 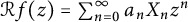be its randomization induced by a standard sequence 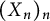of independent Bernoulli, Steinhaus, or Gaussian random variables. In this paper, we characterize those functions 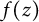such that 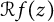is almost surely in the Fock space 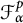for any 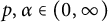. Then such a characterization, together with embedding theorems which are of independent interests, is used to obtain a Littlewood-type theorem, also known as regularity improvement under randomization within the scale of Fock spaces. Other results obtained in this paper include: (a) a characterization of random analytic functions in the mixed-norm space 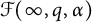, an endpoint version of Fock spaces, via entropy integrals; (b) a complete description of random lacunary elements in Fock spaces; and (c) a complete description of random multipliers between different Fock spaces.

The classical Gelfand–Naimark theorems provide important insight into the structure of general and of commutative 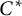-algebras. It is shown that these can be generalized to certain ordered -algebras. More precisely, for 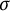-bounded closed ordered -algebras, a faithful representation as operators is constructed. Similarly, for commutative such algebras, a faithful representation as complex-valued functions is constructed if an additional necessary regularity condition is fulfilled. These results generalize the Gelfand–Naimark representation theorems to classes of -algebras larger than 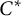-algebras, and which especially contain -algebras of unbounded operators. The key to these representation theorems is a new result for Archimedean ordered vector spaces V: If V is 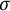-bounded, then the order of V is induced by the extremal positive linear functionals on V.