We study generators of the fundamental group of the group of symplectomorphisms 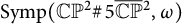 for some particular symplectic forms. It was observed by Kȩdra (2009, Archivum Mathematicum 45) that there are many symplectic 4-manifolds
for some particular symplectic forms. It was observed by Kȩdra (2009, Archivum Mathematicum 45) that there are many symplectic 4-manifolds 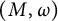 , where M is neither rational nor ruled, that admit no circle action and
, where M is neither rational nor ruled, that admit no circle action and 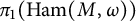 is nontrivial. On the other hand, it follows from Abreu and McDuff (2000, Journal of the American Mathematical Society 13, 971–1009), Anjos and Eden (2019, Michigan Mathematical Journal 68, 71–126), Anjos and Pinsonnault (2013, Mathematische Zeitschrift 275, 245–292), and Pinsonnault (2008, Compositio Mathematica 144, 787–810) that the fundamental group of the group
is nontrivial. On the other hand, it follows from Abreu and McDuff (2000, Journal of the American Mathematical Society 13, 971–1009), Anjos and Eden (2019, Michigan Mathematical Journal 68, 71–126), Anjos and Pinsonnault (2013, Mathematische Zeitschrift 275, 245–292), and Pinsonnault (2008, Compositio Mathematica 144, 787–810) that the fundamental group of the group 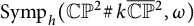 , of symplectomorphisms that act trivially on homology, with
, of symplectomorphisms that act trivially on homology, with 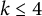 , is generated by circle actions on the manifold. We show that, for some particular symplectic forms
, is generated by circle actions on the manifold. We show that, for some particular symplectic forms 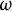 , the set of all Hamiltonian circle actions generates a proper subgroup in
, the set of all Hamiltonian circle actions generates a proper subgroup in 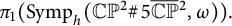 Our work depends on Delzant classification of toric symplectic manifolds, Karshon’s classification of Hamiltonian
Our work depends on Delzant classification of toric symplectic manifolds, Karshon’s classification of Hamiltonian 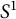 -spaces, and the computation of Seidel elements of some circle actions.
-spaces, and the computation of Seidel elements of some circle actions.
Category Archives: Canadian Journal of Mathematics
On ternary Diophantine equations of signature $(p,p,\text{3})$ over number fields
In this paper, we prove results about solutions of the Diophantine equation 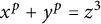 over various number fields using the modular method. First, by assuming some standard modularity conjecture, we prove an asymptotic result for general number fields of narrow class number one satisfying some technical conditions. Second, we show that there is an explicit bound such that the equation
over various number fields using the modular method. First, by assuming some standard modularity conjecture, we prove an asymptotic result for general number fields of narrow class number one satisfying some technical conditions. Second, we show that there is an explicit bound such that the equation 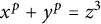 does not have a particular type of solution over
does not have a particular type of solution over 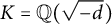 , where
, where 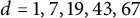 whenever p is bigger than this bound. During the course of the proof, we prove various results about the irreducibility of Galois representations, image of inertia groups, and Bianchi newforms.
whenever p is bigger than this bound. During the course of the proof, we prove various results about the irreducibility of Galois representations, image of inertia groups, and Bianchi newforms.
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
Let G be a p-adic classical group. The representations in a given Bernstein component can be viewed as modules for the corresponding Hecke algebra—the endomorphism algebra of a pro-generator of the given component. Using Heiermann’s construction of these algebras, we describe the Bernstein components of the Gelfand–Graev representation for 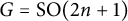 ,
, 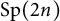 , and
, and 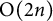 .
.
Singular boundary conditions for Sturm–Liouville operators via perturbation theory
We show that all self-adjoint extensions of semibounded Sturm–Liouville operators with limit-circle endpoint(s) can be obtained via an additive singular form-bounded self-adjoint perturbation of rank equal to the deficiency indices, say 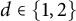 . This characterization generalizes the well-known analog for semibounded Sturm–Liouville operators with regular endpoints. Explicitly, every self-adjoint extension of the minimal operator can be written as
. This characterization generalizes the well-known analog for semibounded Sturm–Liouville operators with regular endpoints. Explicitly, every self-adjoint extension of the minimal operator can be written as 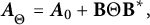
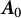 is a distinguished self-adjoint extension and
is a distinguished self-adjoint extension and  is a self-adjoint linear relation in
is a self-adjoint linear relation in 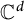 . The perturbation is singular in the sense that it does not belong to the underlying Hilbert space but is form-bounded with respect to
. The perturbation is singular in the sense that it does not belong to the underlying Hilbert space but is form-bounded with respect to 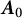 , i.e., it belongs to
, i.e., it belongs to 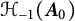 , with possible “infinite coupling.” A boundary triple and compatible boundary pair for the symmetric operator are constructed to ensure that the perturbation is well defined and self-adjoint extensions are in a one-to-one correspondence with self-adjoint relations
, with possible “infinite coupling.” A boundary triple and compatible boundary pair for the symmetric operator are constructed to ensure that the perturbation is well defined and self-adjoint extensions are in a one-to-one correspondence with self-adjoint relations  .
.
The merging of boundary triples with perturbation theory provides a more holistic view of the operator’s matrix-valued spectral measures: identifying not just the location of the spectrum, but also certain directional information.
As an example, self-adjoint extensions of the classical Jacobi differential equation (which has two limit-circle endpoints) are obtained, and their spectra are analyzed with tools both from the theory of boundary triples and perturbation theory.
Quivers with potentials for Grassmannian cluster algebras
We consider a quiver with potential (QP) 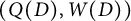 and an iced quiver with potential (IQP)
and an iced quiver with potential (IQP) 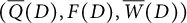 associated with a Postnikov Diagram D and prove that their mutations are compatible with the geometric exchanges of D. This ensures that we may define a QP
associated with a Postnikov Diagram D and prove that their mutations are compatible with the geometric exchanges of D. This ensures that we may define a QP 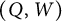 and an IQP
and an IQP 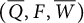 for a Grassmannian cluster algebra up to mutation equivalence. It shows that
for a Grassmannian cluster algebra up to mutation equivalence. It shows that 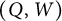 is always rigid (thus nondegenerate) and Jacobi-finite. Moreover, in fact, we show that it is the unique nondegenerate (thus rigid) QP by using a general result of Geiß, Labardini-Fragoso, and Schröer (2016, Advances in Mathematics 290, 364–452).
is always rigid (thus nondegenerate) and Jacobi-finite. Moreover, in fact, we show that it is the unique nondegenerate (thus rigid) QP by using a general result of Geiß, Labardini-Fragoso, and Schröer (2016, Advances in Mathematics 290, 364–452).
Then we show that, within the mutation class of the QP for a Grassmannian cluster algebra, the quivers determine the potentials up to right equivalence. As an application, we verify that the auto-equivalence group of the generalized cluster category 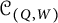 is isomorphic to the cluster automorphism group of the associated Grassmannian cluster algebra
is isomorphic to the cluster automorphism group of the associated Grassmannian cluster algebra 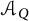 with trivial coefficients.
with trivial coefficients.
The generator rank of subhomogeneous $C^*\!$-algebras
We compute the generator rank of a subhomogeneous 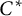 -algebra in terms of the covering dimension of the pieces of its primitive ideal space corresponding to irreducible representations of a fixed dimension. We deduce that every
-algebra in terms of the covering dimension of the pieces of its primitive ideal space corresponding to irreducible representations of a fixed dimension. We deduce that every 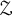 -stable approximately subhomogeneous algebra has generator rank one, which means that a generic element in such an algebra is a generator.
-stable approximately subhomogeneous algebra has generator rank one, which means that a generic element in such an algebra is a generator.
This leads to a strong solution of the generator problem for classifiable, simple, nuclear 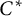 -algebras: a generic element in each such algebra is a generator. Examples of Villadsen show that this is not the case for all separable, simple, nuclear
-algebras: a generic element in each such algebra is a generator. Examples of Villadsen show that this is not the case for all separable, simple, nuclear 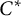 -algebras.
-algebras.
Totally nonnegative Grassmannians, Grassmann necklaces, and quiver Grassmannians
Postnikov constructed a cellular decomposition of the totally nonnegative Grassmannians. The poset of cells can be described (in particular) via Grassmann necklaces. We study certain quiver Grassmannians for the cyclic quiver admitting a cellular decomposition, whose cells are naturally labeled by Grassmann necklaces. We show that the posets of cells coincide with the reversed cell posets of the cellular decomposition of the totally nonnegative Grassmannians. We investigate algebro-geometric and combinatorial properties of these quiver Grassmannians. In particular, we describe the irreducible components, study the action of the automorphism groups of the underlying representations, and describe the moment graphs. We also construct a resolution of singularities for each irreducible component; the resolutions are defined as quiver Grassmannians for an extended cyclic quiver.
Tropical moments of tropical Jacobians
Each metric graph has canonically associated to it a polarized real torus called its tropical Jacobian. A fundamental real-valued invariant associated to each polarized real torus is its tropical moment. We give an explicit and efficiently computable formula for the tropical moment of a tropical Jacobian in terms of potential theory on the underlying metric graph. We show that there exists a universal linear relation between the tropical moment, a certain capacity called the tau invariant, and the total length of a metric graph. To put our formula in a broader context, we relate our work to the computation of heights attached to principally polarized abelian varieties.
